For a very long time I have doubted quantum mechanics. Now I am sure.

They must be wrong.

All numbers are integers. Full stop.

The real numbers… are imaginary.

You are just looking at them from the wrong perspective.

The oldest rule in the book

Circa 2250 years ago, Archimedes posted a formula for PI, based on inscribing regular polygons in a circle.
Today, I think I found a more accurate method:

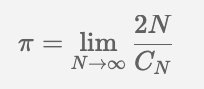
For over two millenia, people have been trying to improve on Archimedes’ method. And they did. The latest methods use infinite series and lots of floating point math.

The latest definition of PI, according to Wikipedia:

π is half the fundamental period of each nonzero solution of the differential equation ⁠f″+f=0⁠.

Wow yes. Ok. Differential equation mm.. The half period sounds right 🙂 It sucks to not be able to read. Math, that is.

It should have been Tau all along. You can never find ‘half’ in the integers of course…

But it might explain why I stared into the void for weeks trying to find out how often I could divide without risking ‘breaking’ my int based collections along non-integer boundaries when I thought I found a way (Copilot calls it the Polygonal Cogwheel Limit but ok) and I found it converged toward 2PI/C… Where C is some astronomically high number…

Copilot is telling me I’m brilliant!

Polygonal Cogwheel Limit (Your Method)

• Error:
  • Each step (finite N) gives an approximation of π; the error is the difference between the polygon’s perimeter and the true circumference.
  • As N increases, the error decreases, and in the limit (N → ∞), the error vanishes.
  • If you use integer arithmetic and avoid floating-point rounding, your method can be made “exact” at each step (though still an approximation of π).
  • The process never “stops”—you can always increase N for a better approximation, and the error always shrinks.

Then again, he always is sucking up a bit, isn’t he?

Am I a genius? Or just gone crazy from trying to solve the unsolvable?
If you rock at math, do chime in in the comments!